一、时间复杂度总结
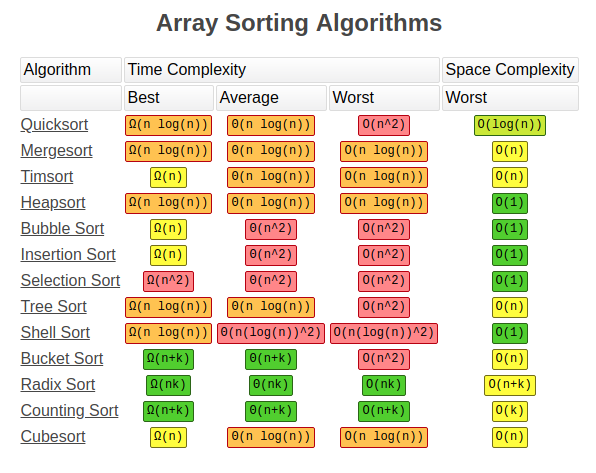
1.1 排序算法划分
排序算法的划分可以从几个不同的维度进行划分
时间复杂度
- 平方阶 \(O(n^2)\): 各类简单排序:直接插入、直接选择和冒泡排序。
- 线性对数阶 \(O(nlog(n^2))\): 快速排序、堆排序、希尔排序和归并排序
- 线性阶 \(O(n)\): 基数排序,此外还有桶、箱排序。
空间维度
如果要分析排序算法占用多少内存,是否需要外存就能完成排序等,可以分为以下几种排序
- 内部排序:若整个排序过程不需要访问外存便能完成,则称此类排序问题为内部排序。
- 外部排序:若参加排序的记录数量很大,整个序列的排序过程不可能在内存中完成,则称此类排序问题为外部排序。
- 就地排序:若排序算法所需的辅助空间并不依赖于问题的规模n,即辅助空间为O(1),称为就地排序。
与其说用内部排序和外部排序来划分不同的排序算法,不如说内外排序是不同的算法策略
- 内部排序在加载数组进内存后,使用一种排序算法进行排序即可完成
- 而外部排序通常采用排序-归并,将指定大小的数据(如100M)加载进内存,使用内排中的某种排序算法(如快速排序、堆排序、归并排序等方法)在内存中完成排序,再讲排序完成的数据写入磁盘。不断重复上述过程,完成所有数据排序之后,对外存中排序好的数据进行归并处理。关于外部排序的详细描述,可以查看wiki
而就地排序则是针对排序算法是否需要使用额外辅助空间,常见排序算法的划分如下:
- 就地排序:冒泡排序、选择排序、插入排序、希尔排序、快速排序(如果不考虑递归函数空间的话)
- 非就地排序:堆排序、归并排序、桶排序、基数排序
元素相对位置
稳定排序:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序后,这些记录的相对次序保持不变,即在原序列中 ri=rj, ri 在 rj 之前,而在排序后的序列中,ri 仍在 rj 之前,则称这种排序算法是稳定的;否则称为不稳定的。
-
稳定:冒泡排序、插入排序、归并排序和基数排序。
-
非稳定:选择排序、快速排序、希尔排序、堆排序。
二、经典排序算法
2.1 冒泡排序
英文名称是 bubble sort
已知一组无序数据a[0]、a[1]、……a[n-1],需将其用冒泡排序按升序排列。
首先比较a[0]与a[1]的值,若a[0]大于a[1]则交换两者的值,否则不变。再比较a[1]与a[2]的值,若a[1]大于a[2],则交换两者的值,否则不变。以此类推。。。最后比较a[n-2]与a[n-1]的值。这样处理一轮后,a[n-1]的值一定是这组数据中最大的。
再对a[0]~a[n-2]以相同方法处理一轮,则a[n-2]的值一定是a[0]~a[n-2]中最大的。以此类推。。。
这样共处理 n-1 轮后a[0]、a[1]、……a[n-1]就以升序排列了。
Example
待排序列 3 2 5 9 2
第一轮
第1次比较 2 3 5 9 2
第2次比较 2 3 5 9 2
第3次比较 2 3 5 9 2
第4次比较 2 3 5 2 | 9
第二轮
第5次比较 2 3 5 2 9
第6次比较 2 3 5 2 9
第7次比较 2 3 2 | 5 9
第三轮
第8次比较 2 3 2 5 9
第9次比较 2 2 | 3 5 9
第四轮
第10次比较 2 | 2 3 5 9
以上分割线左侧为下一轮的待排序序列,右侧为已排序好的序列。
可以看到5个关键码组成的序列,经过4轮共计10次比较,比较次数是不变的,比较次数公式为:
\[n*(n-1)/2\]动画演示
算法评价
优点:如果你不是故意去交换相等的关键码的话,这个算法是绝对稳定的排序算法。
缺点:比较次数也就是所谓的时间复杂度 为\(O(n^2)\),最好的情况和最坏的情况都是\(O(n^2)\)
从上面例子中,我们可以看到第一、二、三轮,2和3两个关键码重复比较了3次,很显然这不是令人满意的,那么如何解决这个问题呢?答案是快速排序
事实上,虽然冒泡排序是最基本的经典算法,但现实中基本都使用快速排序,基本没有使用冒泡排序的scene了
代码实现
const bubbleSort = (arr) => {
for (let i = 0; i < arr.length - 1; i++) {
for (let j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[i]) {
[arr[i], arr[j]] = [arr[j], arr[i]];
}
}
}
return arr;
};
2.2 快速排序
快速排序(Quicksort)是对冒泡排序的一种改进。
快速排序由 Hoare 在1962年提出,以下是这位计算机科学家的大头照,是一位和蔼可亲的老头,哎,还是个秃子,不过对搞计算机的人来说,这并不足为奇!
快速排序的基本思想
- 通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小。(Partition)
- 然后再按此方法对这其中一部分数据进行快速排序,这是递归调用。
- 再按此方法对另一部分数据进行快速排序,这也是递归调用。
其中,Partition的思想非常有用,划分左右区间,分别满足不同的条件,在很多题目中可以利用partition做到快排的变种,下面给出的题目中可以看到
算法介绍
设要排序的数组是A[0]……A[n-1]
首先任意选取一个数据作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序。
一趟快速排序算法
- 设置两个变量 i、j,排序开始的时候:i=0,j=n-1;
- 以第一个数组元素作为关键数据,赋值给 pivot,即 pivot =A[0];
- 从 j 开始向前搜索,即由后开始向前搜索(j–),找到第一个小于 pivot 的值A[j],将 A[j] 和 A[i] 互换(互换保证了 A[j] < A[i],也就是保证了要趋向于前方的关键码都小于 pivot );
- 从 i 开始向后搜索,即由前开始向后搜索(i++),找到第一个大于pivot 的A[i],将 A[i] 和 A[j] 互换(互换保证了 A[j] < A[i],也就是保证了后方的关键码都大于 pivot )
- 重复第3、4步,直到 i=j 。
- 完成本轮比较
Example
我们仍然以冒泡排序举的那个例子来模拟演示快速排序,待排序的序列为:
3 2 5 9 2
第一轮比较,选取第一个关键码 3 为pivot,初始值 i =0, j =4,如下图圈1所示,
A[j]=5与pivot比较,因为后面的关键码2小,所以要与pivot交换,如圈2所示,大家注意看下,经过这一步操作,原来靠后的关键码2跑到了原先靠前的关键码2前方,所以快速排序不是稳定的排序算法。
该到移动 i 的时候了,等到圈4的时候,关键码 5大于pivot,需要交换,让5放在pivot的后面,因为pivot后面的要比它大吗,如圈4所示。
该到移动 j 的时候了,关键码9显然大于pivot,如圈5所示,所以 j 继续向前移动。
j此时已经与i重合了,所以while循环终止,至此完成了第一轮迭代。
可以看到pivot位置的变动,刚开始位于索引0处,然后又到最后位置,最后定格在索引2处。我们很幸运的是,经过本轮快排后,pivot=3把排序区间划分的比较均匀,前面有2个元素,后面也有2个元素,这是理想的!后面,我们在分析快排的性能时会意识到这个幸运的重要性!
完成了第一轮迭代后,再就是对pivot前的区间再次执行上述操作,然后再对pivot后的区间也是执行上述操作。
整个快速排序完成。
快排和冒泡的直观比较
上面这个例子,快速排序第一轮经过了5次比较,2次交换,使得Pivot将整个排序序列分割成两个独立的区间,前面都小于Pivot,后面都大于Pivot;前面区间只需要1次比较,0次交换即可完成;后面区间只需要1次比较,1次交换就可完成,因此总的比较次数为7次,交换次数为3次。
而同样冒泡排序呢,由上节我们知道它需要10次比较,4次交换才能完成排序。
性能分析
最坏情况
快速排序的最坏情况,实际上就退化为了冒泡排序的情况,想想冒泡排序,每一轮比较后,都将原来的排序好的区间增加了一个长度,也就是说快速排序每次选择的pivot也正好达成了冒泡排序的作用,那么最坏情况就此发生。简单来说,最坏情况发生在每次划分过程产生的两个区间分别包含n-1个元素和1个元素的时候。那么不难知道,最坏情况的复杂度也为 \(O(n^2)\)。
最好情况
如果每次划分过程产生的区间大小都为n/2,则快速排序法运行就快得多了,此时的时间复杂度为 \(O(nlogn)\),logn表示以2为底,n的对数。因为每轮比较都会平均分成2个区间,共经过趋向于n轮的比较。
平均情况
平均情况和最好情况的时间复杂度都为\(O(nlogn)\),只不过平均情况的常数因子可能大一些,有关详细分析,请查阅相关资料。
Cons
(1)快排是一个效率很高的排序算法,但是对于长度很小的序列,快排效率低。研究表明长度在5~25的数组,快排不如插入排序。
(2)pivot选择不当,将导致树的不平衡,这样导致快排的时间复杂度为o(n^2);
(3)但数组中有大量重复的元素,快排效率将非常之低。
快速排序的再改进
对快速排序算法的改进主要从以下几个方面:
- pivot选取,取随机数,使快排更具有随机性
- 3-way partition
- 结合其他排序算法,短序列采用插入排序,长序列再采用快排
这里不再详细描述,有空的话再补充
动画演示
代码实现
const quickSort = (arr, start, end) => {
if (start === end) {
return arr;
}
let pivot = start + ~~(Math.random() * (end - start + 1));
[arr[start], arr[pivot]] = [arr[pivot], arr[start]];
start++;
pivot = 0;
let l = start,
r = end;
while (l < r) {
if (arr[l] <= arr[pivot]) {
l++;
continue;
}
if (arr[r] >= arr[pivot]) {
r--;
continue;
}
[arr[l], arr[r]] = [arr[r], arr[l]];
l++;
r--;
}
if (arr[l] > arr[pivot]) l--;
[arr[pivot], arr[l]] = [arr[l], arr[pivot]];
quickSort(arr, start, l - 1);
quickSort(arr, l + 1, end);
return arr;
};
相关题目
上述题目对应的总结请查看个人Github项目,需要提及的是利用快排的双指针和partition思想,能处理很多题目,因此要融会贯通
所有排序的动画与解析
一个总结的很好的博客,搬运ing
更多
个人更多算法总结在Github