前言
由于实际生产中,输入数据通常会呈现数量级的增长,为了更好的衡量算法性能对系统本身造成的影响,就要分析算法以输入数量n为衡量标准的时间开销和内存/存储开销,即所谓的时间复杂度和空间复杂度。
概念
算法的时间复杂度(Time Complexity),用来度量算法的运行时间,记作: T(n) = O(f(n))。它表示随着 输入大小n 的增大,算法执行需要的时间的增长速度可以用 f(n) 来描述。
算法的空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度,记做S(n)=O(f(n))。比如直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度了,因为每次递归函数要单独开辟函数的空间,存储函数局部变量、返回值等信息。因此要尽量避免使用递归
表示方法:
- 大O表示法
代码的运行时间,和运行的指令次数成正比: \(T(n)=O(f(n))\)
- T(n) 是所有代码的执行时间
- n 表示数据规模的大小
- f(n) 表示一行一行代码执行次数的总和
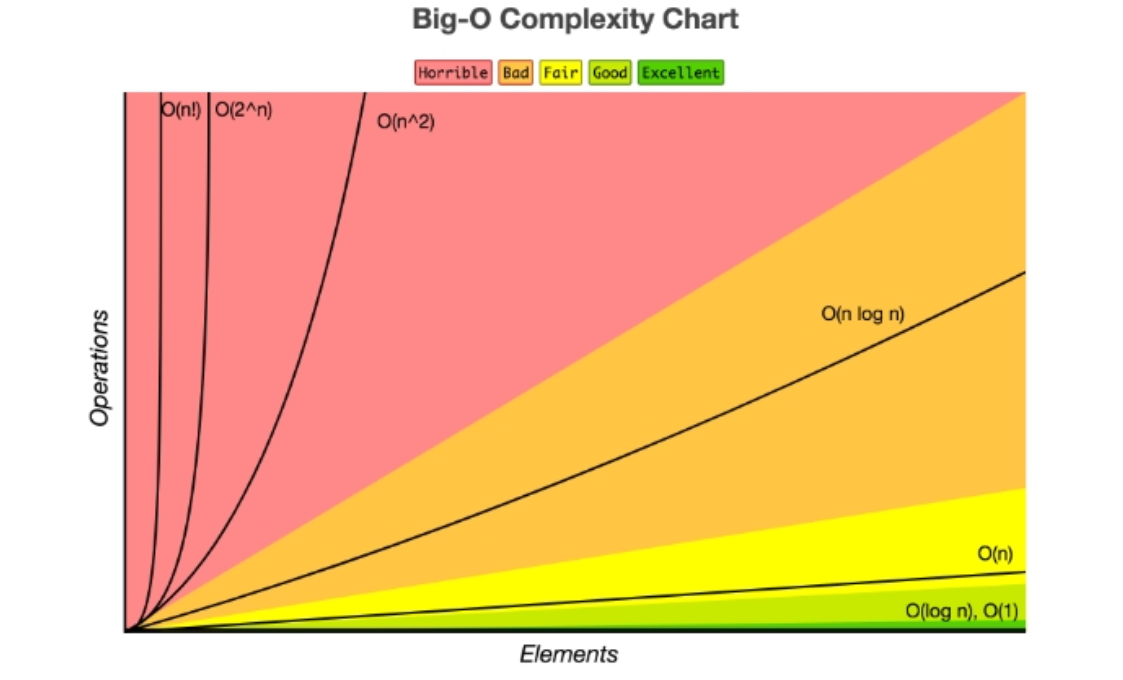
常见的大O复杂度
- 其他表示方法:Omega(\(\omega\))、Theta(\(\theta\))等
大O表示法最为常用,但也存在大Ω表示法和大Θ表示法等,它们的区别这篇文章描述的很清晰,在此就不赘述了
O(1):常量阶
所有的代码的执行次数是一个定值, 无论多大多小, 只要不随 n 的增大而增大, 这样的代码复杂度就是 O(1)
// O(1)
int k = 100;
// O(1)
const long long f = 10000000000000000000000000000;
for(int i = 0; i < f; ++i)
{
}
O(log n):对数阶
数据从起始状态, 以乘法的形式向上生长去接近 n, 其时间复杂度就是 O(logn) O(\log n)O(logn)
int i = 1;
while(i <= n)
i = i * 2;
O(n):线性阶
与n成正比,自然是n层循环啦
int i = 0;
while( i < n)
printf("%d \n",i);
O(nlog n):线性对数阶
O(nlogn) 自然就是 一段 O(logn) 的代码, loop 了 n次. 之所以将这个复合府再度单提出来, 是因为这个 O(nlogn) 复杂度很常见, 比如归并排序, 快排等等.
O(\(n^k\)):k次方阶
例如O(\(n^2\)),O(\(n^3\)),实际上就是k层循环的嵌套
O(\(2^n\)):指数阶
增长非常迅速,绝对要避免
O(n!):阶乘阶:
最恐怖的复杂度,如果你写出来这样的代码,恭喜你,向上面的时间复杂度改进吧!(捂脸)
空间复杂度
上述大O表示法的分析是以时间复杂度为例,空间复杂度则用类似的思路考虑存储空间的消耗即可。通常更关注时间复杂度,不过在一些项目中可能存在特定的要求,尽量减少存储消耗,这种时候就要考虑空间复杂度了~
参考
作者:鹅城惊喜师爷 来源:CSDN 原文:https://blog.csdn.net/baishuo8/article/details/82903000 版权声明:本文为博主原创文章,转载请附上博文链接!